P-form electrodynamics
In theoretical physics, p-form electrodynamics is a generalization of Maxwell's theory of electromagnetism.
Contents |
Ordinary (viz. one-form) Abelian electrodynamics
We have a one-form A, a gauge symmetry
where α is any arbitrary fixed 0-form and d is the exterior derivative, and a gauge-invariant vector current J with density 1 satisfying the continuity equation
where * is the Hodge dual.
Alternatively, we may express J as a (d − 1)-closed form.
F is a gauge invariant 2-form defined as the exterior derivative 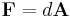 .
.
A satisfies the equation of motion
(this equation obviously implies the continuity equation).
This can be derived from the action
where M is the spacetime manifold.
p-form Abelian electrodynamics
We have a p-form B, a gauge symmetry
where α is any arbitrary fixed (p-1)-form and d is the exterior derivative,
and a gauge-invariant p-vector J with density 1 satisfying the continuity equation
where * is the Hodge dual.
Alternatively, we may express J as a (d-p)-closed form.
C is a gauge invariant (p+1)-form defined as the exterior derivative 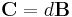 .
.
B satisfies the equation of motion
(this equation obviously implies the continuity equation).
This can be derived from the action
where M is the spacetime manifold.
Other sign conventions do exist.
The Kalb-Ramond field is an example with p=2 in string theory; the Ramond-Ramond fields whose charged sources are D-branes are examples for all values of p. In 11d supergravity or M-theory, we have a 3-form electrodynamics.
Non-abelian generalization
Just as we have non-abelian generalizations of electrodynamics, leading to Yang-Mills theories, we also have nonabelian generalizations of p-form electrodynamics. They typically require the use of gerbes.
References
- Henneaux; Teitelboim (1986), "p-Form electrodynamics", Foundations of Physics 16 (7): 593-617, doi:10.1007/BF01889624
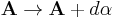
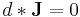
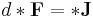
![S=\int_M \left[\frac{1}{2}\mathbf{F}\wedge *\mathbf{F} - \mathbf{A} \wedge *\mathbf{J}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/7e2bfd78e103e72c813c6c0818e036f2.png)
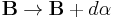
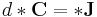
![S=\int_M \left[\frac{1}{2}\mathbf{C}\wedge *\mathbf{C} %2B(-1)^p \mathbf{B} \wedge *\mathbf{J}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/8641c297b7759ddb66ab523fa8895afb.png)